Trees &
Binary Trees
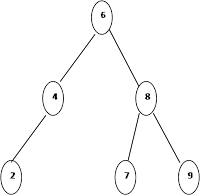
A
tree is a non linear data structure.
A
tree consists of nodes connected by edges. The nodes are
represented as circles, and the
edges as lines connecting the circles.
There are different kinds of trees:
multiway trees, binary
trees etc.
Many terms are used to describe particular
aspects of trees. They are:
Path
The
sequence of nodes along the edges that connect them is called a path.
Root
The
node at the top of the tree is called the root. There is only one root in a tree. In a tree, there must be one
(and only one!) path from the root to any other node.
Parent
Any
node (except the root) has exactly one edge running upward to another node.
The
node above it is called the parent of
the node.
Child
Any
node may have one or more lines running downward to other nodes. These
nodes
below a given node are called its children.
Leaf
A
node that has no children is called a leaf node or simply a leaf.
There can be only
one
root in a tree, but there can be many leaves.
Subtree
Any
node may be considered to be the root of a subtree, which consists of its children,
and
its children’s children, and so on.
Visiting
A
node is visited
when program control arrives at the node,
usually for the purpose of
carrying
out some operation on the node, such as checking the value of one of its
data
fields or displaying it.
Traversing
To
traverse
a tree means to visit all the nodes in some
specified order. For example,
we
might visit all the nodes in order of ascending key value.
Levels
The
level
of a particular node refers to how many
generations the node is from the
root.
If we assume the root is Level 0, then its children will be Level 1, its
grandchildren
will
be Level 2, and so on.
Keys
In
tree diagrams, when a circle represents a node holding a data item, the key
value of the
item
is typically shown in the circle. This key value is used to search for the item
or perform other operations on it.
Binary
Trees
If
every node in a tree can have at most two children, the tree is called a binary tree.
The
two children of each node in a binary tree are called the left child and the right
Child.
A node in a binary tree may have both the children, only a left child, or only a right child, or it can have no children at all (in which case it’s a leaf).
Binary search tree
Is
a kind of binary tree.
The defining characteristic of a
binary search tree is: A node’s left child must have a key
less than its parent, and a
node’s right child must have a key greater than or equal to its
parent.
The
different operations on binary search tree are:
Ø
Inserting a node
Ø
Finding a node
Ø
Deleting a node
Ø
Traversing a tree
Ø
Finding a minimum & maximum value.
Finding a node:
Let
the value to be found is the key value say 57.
We know that the defining characteristic
of a binary search tree is: A node’s left child must have a key less than its
parent, and a node’s right child must have a key greater than or equal to its parent.
Finding node starts at the root. The
program compares the key value 57
with
the value at the root, which is 63. The key is less, so the program knows the
desired
node must be on the left side of the tree—either the root’s left child or one
of
this
child’s descendants. The left child of the root has the value 27, so the
comparison
of
57 and 27 will show that the desired node is in the right subtree of 27. The
arrow
will go to 51, the root of this subtree. Here, 57 is again greater than the 51
node,
so we go to the right, to 58, and then to the left, to 57. This time the
comparison
shows
57 equals the node’s key value, so we’ve found the node we want.
Code for the find() function:
public
Node find(int key) // find node with given key
{ // (assumes non-empty tree)
Node current = root; // start at root
while(current.iData != key) //
while no match,
{
if(key < current.iData) // go left?
current = current.leftChild;
else
current = current.rightChild; // or go right?
if(current == null) // if no child,
return null; // didn’t find it
}
return current; // found it
}
Inserting a Node :
To
insert a node we must first find a place to insert it. This is much the same process
as trying to find a node that turns out not to exist. ie; We follow the path from the root to the
appropriate node, which will be the parent of the new node. When this parent is
found, the new node is connected as its left or right child, depending on
whether the new node’s key is less or greater than that of the parent.
Example:
Let’s
assume we’re going to insert a new node with the value 45. The first step for
the program in inserting a node is to find where it should be inserted. The
value 45 is less than 60 but greater than 40, so we arrive at node 50. Now we want
to go left because 45 is less than 50, but 50 has no left child; its leftChild
field is null. When it sees this null, the insertion routine has found the
place to attach the new node. A new node is created with the value 45 and
connects it as the left child of 50.
Code for the insert() function:
public
void insert(int id, double dd)
{
Node newNode = new Node(); // make new node
newNode.iData = id; // insert data
newNode.dData = dd;
if(root==null) // no node in root
root = newNode;
else // root occupied
{
Node current = root; // start at root
Node parent;
while(true) //
(exits internally)
{
parent = current;
if(id < current.iData) // go left?
{
current = current.leftChild;
if(current == null) // if end of the line,
{ //
insert on left
parent.leftChild
= newNode;
return;
}
} //
end if go left
else //
or go right?
{
current =
current.rightChild;
if(current == null) // if end of the line
{ // insert on
right
parent.rightChild
= newNode;
return;
}
} //
end else go right
} //
end while
} //
end else not root
}
//
end insert()
Deleting a Node
Deleting
a node is the most complicated common operation required for binary
search
trees.
We
start by finding the node we want to delete, using the same approach we saw
in
find() and insert(). When we have found the node, there are three cases to
consider:
1. The node to be deleted is a leaf (has no
children).
2. The node to be deleted has one child.
3. The node to be deleted has two children.
Case 1: The Node to Be Deleted Has No Children
To
delete a leaf node, you simply change the appropriate child field in the node’s
parent
to point to null, instead of to the node. The node will still exist, but it
will no
longer
be part of the tree.
Example:
Assume
we are going to delete node 7. The first part of the delete() routine is
similar to find() and insert(). It involves finding the node to be deleted. As
with insert(), we need to remember the parent of the node to be deleted so we
can modify its child fields. If we find the node, we drop out of the while loop
with parent containing the node to be deleted. If we can’t find it, we return
from delete() with a value of false.
public
boolean delete(int key) //
delete node with given key
{
// (assumes non-empty list)
Node current = root;
Node parent = root;
boolean isLeftChild = true;
while(current.iData != key) // search for node
{
parent = current;
if(key < current.iData)
// go left?
{
isLeftChild = true;
current = current.leftChild;
}
else //
or go right?
{
isLeftChild = false;
current = current.rightChild;
}
if(current == null) //
end of the line,
return false; // didn’t find it
} //
end while
//
found node to delete continues...
}
After
we’ve found the node, we check first to verify
that it has no children. When
this
is true, we check the special case of the root. If that’s the node to be deleted, we
simply
set it to null; this empties the tree. Otherwise, we set the parent’s leftChild or
rightChild
field to null to disconnect the parent from the node.
//
delete() continued...
//
if no children, simply delete it
if(current.leftChild==null && current.rightChild==null)
{
if(current == root) // if root,
root = null; // tree is empty
else if(isLeftChild)
parent.leftChild = null; // disconnect
else //
from parent
parent.rightChild = null;
}
Graph Traversal
The
breadth first search (BFS) and the depth first search (DFS) are the two
algorithms used for traversing and searching a node in a graph. They can also
be used to find out whether a node is reachable from a given node or not.
Depth First Search
(DFS)
The
aim of DFS algorithm is to traverse the graph in such a way that it tries to go
far from the root node. Stack is used in the implementation of the depth first
search. Let’s see how depth first search works with respect to the following
graph:
As
stated before, in DFS, nodes are visited by going through the depth of the tree
from the starting node.
If we do the depth first traversal of the above graph and print the visited node, it will be “A B E F C D”. DFS visits the root node and then its children nodes until it reaches the end node, i.e. E and F nodes, then moves up to the parent nodes.
If we do the depth first traversal of the above graph and print the visited node, it will be “A B E F C D”. DFS visits the root node and then its children nodes until it reaches the end node, i.e. E and F nodes, then moves up to the parent nodes.
Algorithmic Steps
1. Step 1: Push the root node in the
Stack.
2. Step 2: Loop until stack is empty.
3. Step 3: Peek the node of the
stack.
4. Step 4: If the node has unvisited child nodes,
get the unvisited child node, mark it as traversed and push it on
stack.
5. Step 5: If the node does not have any
unvisited child nodes, pop the node from the stack.
Based
upon the above steps, the following Java
code shows the implementation of the DFS algorithm:
//
public void dfs()
{
//DFS uses
Stack data structure
Stack s=new
Stack();
s.push(this.rootNode);
rootNode.visited=true;
printNode(rootNode);
while(!s.isEmpty())
{
Node
n=(Node)s.peek();
Node
child=getUnvisitedChildNode(n);
if(child!=null)
{
child.visited=true;
printNode(child);
s.push(child);
}
else
{
s.pop();
}
}
//Clear
visited property of nodes
clearNodes();
}
//
Breadth First Search
(BFS)
This
is a very different approach for traversing the graph nodes. The aim of BFS
algorithm is to traverse the graph as close as possible to the root node. Queue
is used in the implementation of the breadth first search. Let’s see how BFS
traversal works with respect to the following graph:
Algorithmic Steps
1. Step 1: Push the root node in the Queue.
2. Step 2: Loop until the queue is empty.
3. Step 3: Remove the node from the Queue.
4. Step 4: If the removed node has unvisited
child nodes, mark them as visited and insert the unvisited children in the
queue.
Based
upon the above steps, the following Java
code shows the implementation of the BFS algorithm:
//
public void bfs()
{
//BFS uses
Queue data structure
Queue q=new
LinkedList();
q.add(this.rootNode);
printNode(this.rootNode);
rootNode.visited=true;
while(!q.isEmpty())
{
Node
n=(Node)q.remove();
Node
child=null;
while((child=getUnvisitedChildNode(n))!=null)
{
child.visited=true;
printNode(child);
q.add(child);
}
}
//Clear
visited property of nodes
clearNodes();
}
No comments:
Post a Comment